Toán học là một bộ môn vô cùng quan trọng trong giáo dục và đào tạo. Những công thức tính toán được ghi trong sách vở có công dụng rất lớn đối với học tập và cuộc sống hàng ngày. Tam giác là một hình học cơ bản và quan trọng đối với bộ môn này, học sinh cần biết đến những cách tính chiều cao hình tam giác cơ bản để có thể nắm vững kiến thức nhất. Cùng nhan dinh bong da macao theo dõi bài viết dưới dây nhé!
Khái niệm về tam giác
Tam giác là một hình đa giác nằm trong bộ môn hình học, đây là một hình bao gồm ba điểm không thẳng hàng nhau và có ba cạnh nối ba điểm lại với nhau tạo thành một hình hoàn chỉnh. Đây là đa giác có số cạnh ít nhất – chỉ có ba cạnh. Một hình tam giác có tổng số các góc phải bằng 180 độ. Đây là dấu hiệu nhận biết và là cách phân biệt hình tam giác với các đa giác khác.
Định nghĩa về hình tam giác và đường cao
Hình tam giác có các dạng hình sau đây:
- Hình tam giác nhon
- Hình tam giác tù
- Hình tam giác vuông
- Hình tam giác đều
- Hình tam giác cân
- Hình tam giác vuông cân
Đường cao là đường như thế nào trong hình tam giác
Đường cao là đường như thế nào trong hình tam giác
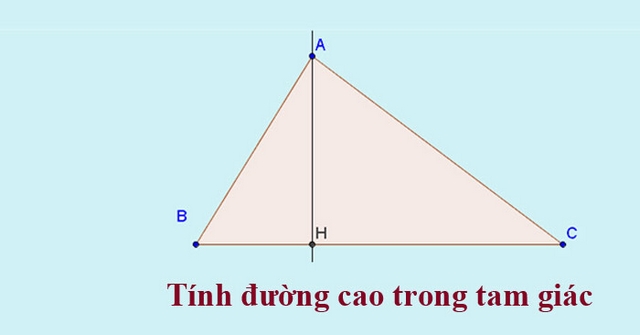
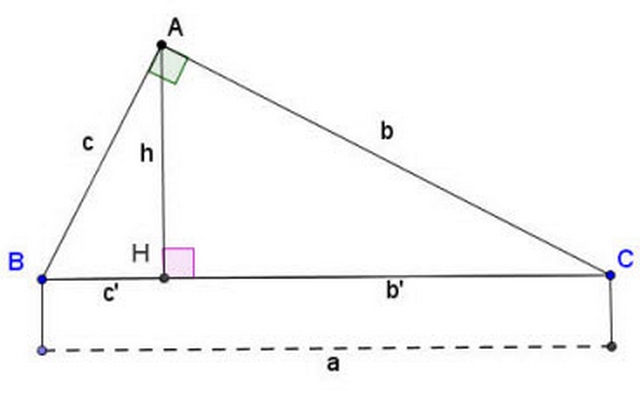
Để có được công thức tính chiều cao hình tam giác các bạn cần biết đến định nghĩa về đường cao trong tam giác. Đây là một đường thẳng kẻ từ một đỉnh bất kỳ và vuông góc với cạnh đối diện. Cạnh đối diện được gọi là đáy tương ứng với đường cao của hình tam giác.
Chân đường cao chính là điểm giao nhau giữa đường cao và cạnh đáy. Cách tính chiều cao hình tam giác chính là tính độ dài của đường thẳng tính từ đỉnh đến cạnh đáy hình tam giác có ký hiệu là h. Độ dài đường cao h còn được áp dụng để tính ra diện tích của một hình tam giác.
Xem thêm >>> Khoa học xã hội là môn gì? Định hướng nghề nghiệp chính xác nhất
Các cách tính chiều cao hình tam giác cơ bản cần biết
Đường cao là một đường thẳng quan trọng trong hình tam giác. Các bạn khi học về hình học này cần biết đến công thức tính chiều cao của hình tam giác của các hình cơ bản và thường xuyên gặp nhất.
Công thức tính chiều cao của hình tam giác thường
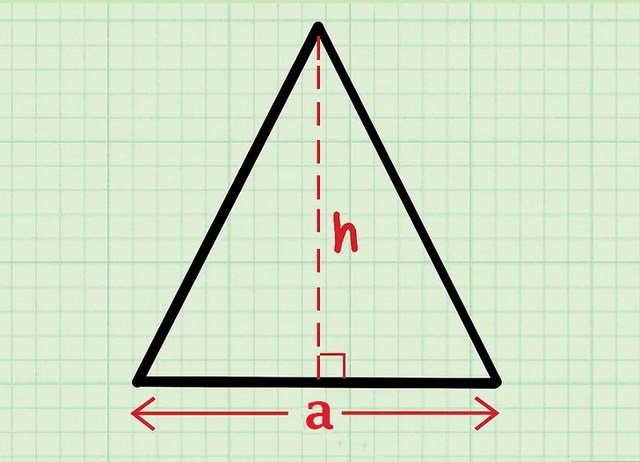
Tam giác thường có một tên gọi khác là tam giác nhọn, đây là hình tam giác cơ bản nhất. Hình này có độ dài các cạnh không giống nhau, số đo các góc phải nhỏ hơn 90 độ và mỗi góc phải có một số đo khác nhau. Chiều cao là một đường thẳng bất kỳ hạ từ đỉnh xuống cạnh đối diện tương xứng.
Cách tính chiều cao của tam giác thường: h= S x 2a hoặc h= S x 2 : a.
Ký hiệu:
- h: chiều cao hình tam giác
- S: diện tích hình tam giác
- a: cạnh đáy hình tam giác
Cách tính chiều cao hình tam giác thường
Cách tính chiều cao của hình tam giác vuông
Tam giác vuông là một tam giác có một góc vuông 90 độ và tổng hai góc còn lại trong hình phải bằng 90 độ. Đây là một hình tam giác đặc biệt khi chiều cao của hình chính là một cạnh góc vuông và cạnh góc vuông còn lại là cạnh đáy của hình tam giác.
Công thức tính chiều cao hình tam giác vuông:
a= S x 2b hoặc b= S x 2a.
Ký hiệu
- S: diện tích đáy hình tam giác vuông
- a và b: chiều cao và cạnh đáy hình tam giác vuông.
Công thức tính chiều cao hình tam giác cân
Tam giác cân là một hình tam giác có hai cạnh bên với độ dài bằng nhau và hai góc liền kề trong hình tam giác có số độ bằng nhau. Cách tính chiều cao hình tam giác cân giống với công thức tính chiều cao của tam giác nhọn.
Công thức tính: h= S x 2a hoặc h= S x 2 : a
Ký hiệu :
- S: diện tích hình tam giác cân
- a: cạnh đáy hình tam giác cân
- h: chiều cao hình tam giác cân
Xem thêm >>> Code tân thủ tập kích và những thông tin cần biết
Công thức tính chiều cao hình tam giác đều
Công thức tính đường cao hình tam giác đều
Tam giác đều là một hình tam giác có chiều dài ba cạnh bằng nhau, số đo độ của 3 góc trong tam giác bằng nhau và mỗi góc đều là 60 độ. Đây là hình tam giác đặc biệt nhất khi có độ dài và số đo độ đều bằng nhau. Chiều cao của hình tam giác cũng là một đường thẳng hạ từ đỉnh xuống đáy.
Cách tính chiều cao hình tam giác đều được chia thành hai trường hợp sau đây:
- Khi đề bài đã cho diện tích tam giác đều thì chiều cao tính:
h= S x 2a hoặc h= S x 2 : a.
- Khi đề bài cho số liệu độ dài một cạnh thì chiều cao tính:
h= a x 32.
Tuy nhiên trong tính chiều cao của hình tam giác đều cách tính ở trường hợp một được áp dụng nhiều và phổ biến hơn so với cách ở trường hợp hai. Đối với cách thứ hai đây là một công thức áp dụng tính dành cho những bài toán nâng cao với yêu cầu phức tạp và độ khó nâng cao hơn. Các bạn có thể tham khảo và áp dụng công thức phù hợp với đề bài đưa ra.
Trên đây là tổng hợp những cách tính chiều cao hình tam giác cơ bản sẽ được giảng dạy trong chương trình học. Hy vọng bài viết của nhan dinh bong da macao sẽ giúp các bạn bổ sung và nắm bắt kiến thức về hình tam giác tốt nhất.